决策树（一）：基础

基本流程

使用不熟悉的数据集合，从中提取出一系列规则，能够对新数据进行分类
极大化信息增益$a_* = argmax_{a\in A}{Gain(D,a)}$

构建决策树伪代码

createBranch()：
    检测数据集中的每个项是否属于同一个分类：
    if so 
       return 类标签
    else
       寻找划分数据集的最好特征***
       划分数据集
       创建分支节点
            for 每个分支节点，递归调用createBranch()函数
        return 分支节点

关键

显然，构建决策树的关键是寻找划分数据集的最好特征，我们希望决策树分支节点包含的样本尽可能属于同一类别——纯度（purity）越高越好

划分选择

1. 信息熵 ——> 信息增益

信息熵

信息论中表示样本的不确定性大小，度量样本集合纯度最常用的指标
样本集合D中第k类占比$p_k$则D的信息熵定义为: $Ent(D)=-\sum\limits_{k=1}^{\left |y\right|}p_{k}log_2p_{k}$

信息增益

假定离散属性a在D中有V个可能的取值${a^1,a^2,…,a^V}$,若依据属性a对D进行分类，产生V个分支点，根据每个分支点样本数量对分支点赋权重$\left |D^V\right|/D$，于是根据属性a进行划分获得的信息增益为：

$Gain(D,a) = Ent(D)-\sum\limits_{v=1}^{\left |v\right|}\frac{\left |D^V\right|}{D}Ent(D^v)$

也就是信息熵的减少量，越大越好：

$a_* = argmax_{a\in A}Gain(D,a)$

接下来如果给出下表中关于西瓜的特征数据，据此判断西瓜的好坏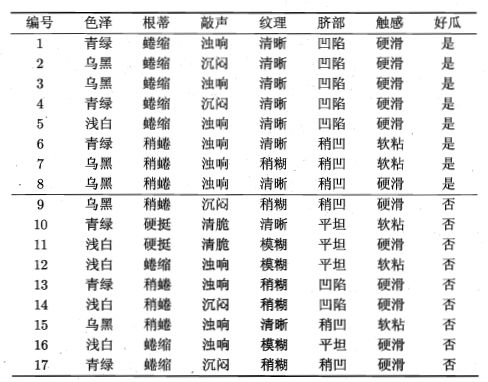

我们就可以先算出根节点的信息熵（分为好、坏两类）——>计算依每一个属性进行划分所获得的信息增益，选取信息增益最大的属性作为分支节点——>重复上述过程直到无法分类。得到如下决策树：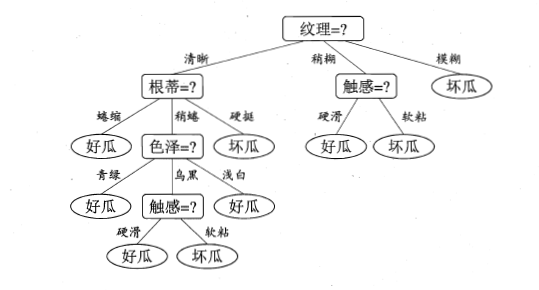

算法

ID3决策树

思考：如果我们将数据中“编号”这一属性也作为一个候选的划分属性，该属性能够产生17个分支，每个分支只包含一个样本，显然纯度最高，所产生的信息增益也最大，但不具备泛化能力。

缺点

实际上信息增益准则对可取值数目较多的属性有所偏好（分的越细致的属性越会得到信息增益准则的偏好），但这种偏好会带来泛化能力差的不利影响。

2. 增益率

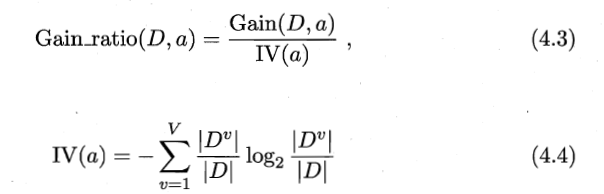
其中IV(a)称为属性a的固有值，属性a的可能取值越多，IV(a)越大，相应地会减小Gain_ration的值。

缺点

与信息增益相反，信息增益准则对可取值数目较少的属性有所偏好，分类性能下降。

C4.5算法

结合信息增益和增益率

step1：在候选属性中找出信息增益高于平均水平的属性
step2：在从中选择增益率最高的

3. 基尼指数

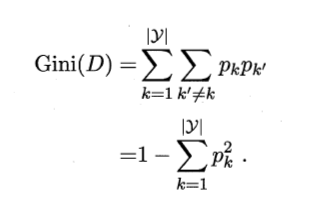
用于度量数据集的纯度，物理意义：从数据集中随机取两个样本，二者不属于同一类别的概率，故Gini值越小，数据集纯度越高。
属性a的Gini值定义如下：

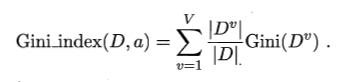
选取使得划分后Gini指数最小的属性作为划分属性，即$a_* = argmax_{a\in A}Gini_index(D,a)$

CART算法

采用Gini指数选择属性分类

剪枝处理

解决问题

过拟合（分支过多，泛化能力差）

方法一：预剪枝

预剪枝是在决策树生成过程中，如果这个节点进行划分，不能带来泛化性能的提升，则停止划分并将该节点设置为叶子节点
缺点：“贪心”策略禁止决策树分支展开，容易导致欠拟合

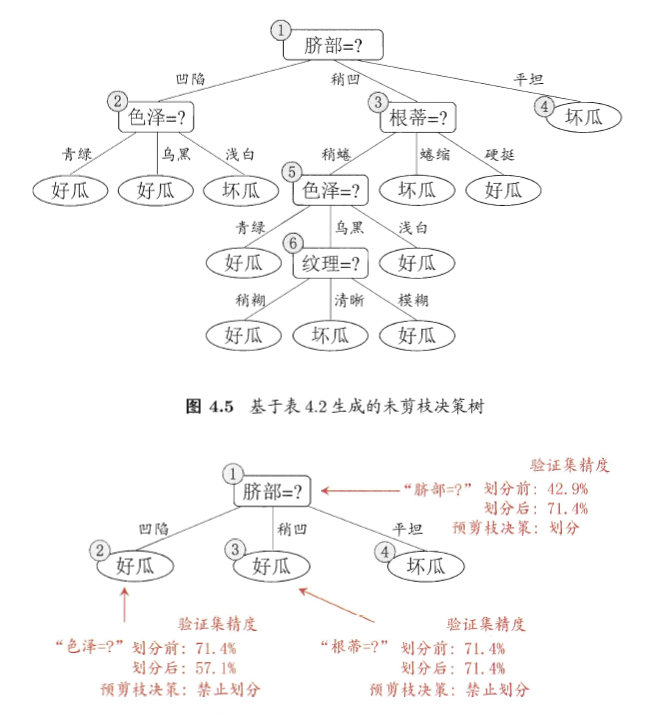
方法二：后剪枝

先训练好一棵树，然后自底向上对非叶子节点进行考察，如果将该节点对应的子树替换为叶节点能不能带来泛化性能的提升，能就将该子树替换为叶节点。
优点：泛化能力好
缺点：时间开销大

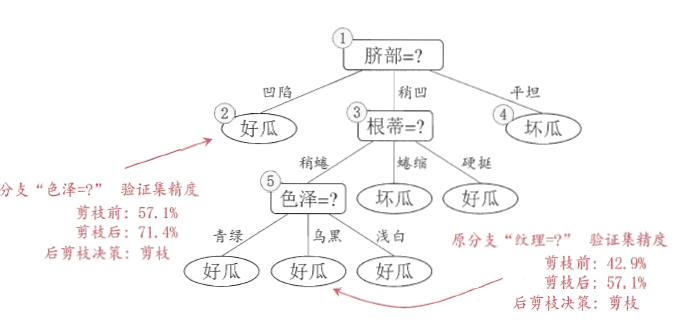
这里的泛化性能利用模型在测试集上的准确率来衡量