【leetcode】476 number complement

刷题第二天，好巧哦又是一道bit manipulation的

题目：

Given a positive integer, output its complement number. The complement strategy is to flip the bits of its binary representation.

Note:
The given integer is guaranteed to fit within the range of a 32-bit signed integer.
You could assume no leading zero bit in the integer’s binary representation.
Example 1:

Input: 5
Output: 2
Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.

Example 2:

Input: 1
Output: 0
Explanation: The binary representation of 1 is 1 (no leading zero bits), and its complement is 0.

The above arrows point to positions where the corresponding bits are different.
Subscribe to see which companies asked this question.

问题陈述：

就是要将一个整数的二进制表示做取反操作，输出取反后的十进制表示。

需要注意的是二进制表示前面的0，比如5的二进制表示是00000101，如果直接取反得到的是11111010，而我们所要求的是不含前面的占位0的取反十进制表示，也就是(00000)010。

题目思路：

1. 首先要求出来输入的整形数字二进制表示的位数n，也就是不含前导0的二进制表达的位数（如5的二进制表达是101，就是三位）
2. 然后将输入数字与n个1做异或操作，就相当于取反了

例：
int = 5， 二进制表达为 00000101，位数为3，与00000111做异或运算得到00000010

第2步很好求，知道了位数n之后，${2^n}-1$就是末位为n个1的十进制表示

关键是第1步求十进制表示所占的位数，最开始我尝试了用数学的方式来求解，但是费尽周折仍有bug，于是乎上网搜了搜，发现可以用向右移位判断是否为0的方法，记录下移动的位数，就是十进制表示所占位数，哎，我怎么就没想到

代码：

class Solution {
public:
    int findComplement(int num) {
        int numm = num;
        int bitnum = 0;
        while (num) {
            bitnum++;
            num = num >> 1;
        }
        int sec = pow(2, bitnum)-1;
        int a = numm^sec; 
        return a;
    }
};

运行结果：

总结：

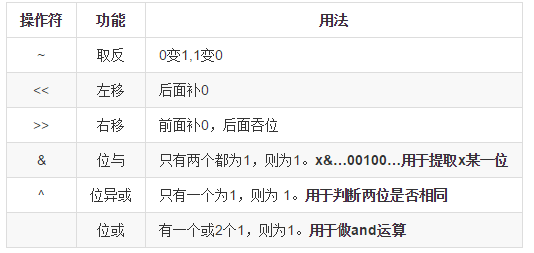
对于二进制的运算以及位操作符还是不够熟练，不能做到手到擒来，看来这个表要牢记在心