背景
FFM(Field-aware Factorization Machine)最初的概念来自Yu-Chin Juan(阮毓钦,毕业于中国台湾大学,现在美国Criteo工作)与其比赛队员,是他们借鉴了来自Michael Jahrer的论文中的field概念提出了FM的升级版模型
原理
线性模型
对于给定的数据我们进行训练,进而对测试集进行预测,首先我们想到利用线性模型进行拟合(也就是一维特征):
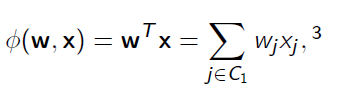
进一步,我们考虑加入二维组合特征进行拟合:
FM
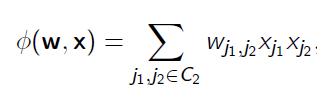
也就是FM中的交叉特征(二次项),采用矩阵分解得到如下形式:
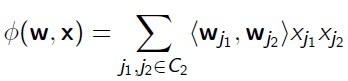
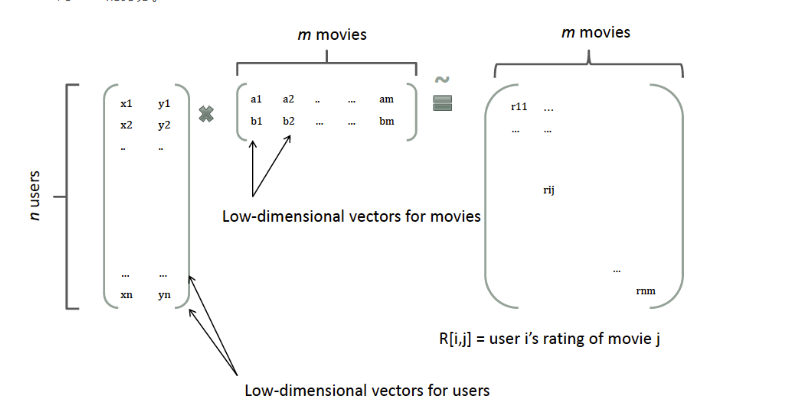
其中$w_{j_1}$和$w_{j_2}$分别为特征$j_1$和$j_1$对应的隐向量,对应下图中左边两个矩阵的一行或一列即是一个隐向量。
FFM
现在在FM的基础之上,我们引入field-aware的概念,可以推得FFM的二次项形式如下:
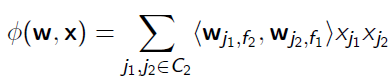
其中$w_{j_1,f_{j_2}}$为特征$j_1$针对$j_2$所在的类别$f_{j_2}$的隐向量
$w_{j_2,f_{j_1}}$为特征$j_2$针对$j_1$所在的类别$f_{j_1}$的隐向量
FFM完整的模型方程为
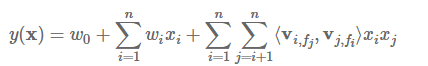
为了便于理解,先看下面的例子
| Clicked? | Country | Day | Ad_type |
|---|---|---|---|
| 1 | USA | 26/11/15 | Movie |
| 0 | China | 1/7/14 | Game |
| Clicked? | Country=USA | Country=China | Day=26/11/15 | Day=1/7/14 | Day=19/2/15 | Ad_type=Movie | Ad_type=Game |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
我们对原始数据进行One-Hot编码生成数值特征,这时引入field的概念,把同一个categorical特征经过One-Hot编码生成的数值特征都放到同一个field中。比如:“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征是由“日期”这一categorical特征生成的,可以放到同一个field中。这时我们再计算隐向量的时候,隐向量不仅与特征相关,还与field相关。每一维特征$x_i$针对其它特征的每一种field
$f_j$,都会学习一个隐向量 $w_{i,f_j}$。
假设样本的n个特征属于 f 个field,那么FFM的二次项有 nf 个隐向量,如果隐向量的长度为 k ,那么FFM的二次参数有 nfk 个。而在FM模型中,每一维特征的隐向量只有一个,FM可以看作FFM的特例,是把所有特征都归属到一个field时的FFM模型。此外,由于隐向量与field相关,FFM二次项并不能够化简,其预测复杂度是 $O(kn^2)$。
FFM实现
Yu-Chin Juan实现了一个C++版的FFM模型,源码可从Github下载https://github.com/guestwalk/libffm
该FFM模型采用logistic loss作为损失函数,和L2惩罚项,因此只能用于二元分类问题。
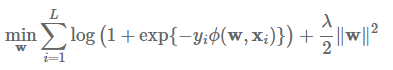
模型采用SGD进行优化。
实例

这条记录可以编码成5个特征,其中“Genre=Comedy”和“Genre=Drama”属于同一个field,“Price”是数值型,不用One-Hot编码转换。
利用线性模型进行拟合:
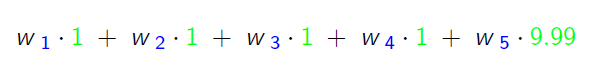
二维组合特征拟合:
FM(隐向量)拟合: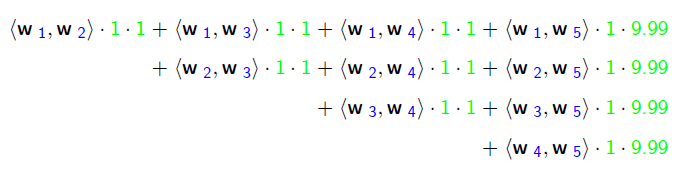
FFM拟合:
为了方便说明FFM的样本格式,我们将所有的特征和对应的field映射成整数编号。
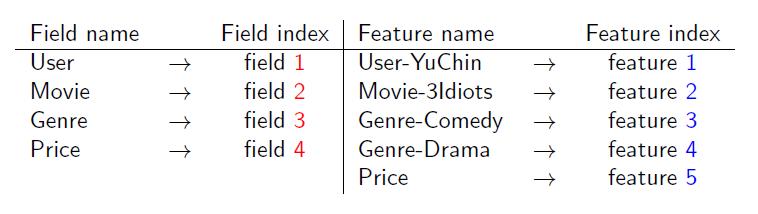
FFM的组合特征有10项,如下图所示