Optimal Real-Time Bidding for Display Advertising——KDD2014
参考着师兄的博客计算广告小窥[中]这孙子怎么什么都知道,仔细读完了这篇paper,总结一下,方便日后回顾
ps:十分感谢师兄@面包包包包包包,看了师兄的三篇博客可算是入了门,不然真是一头雾水hold不住啊
这篇文章的核心就是提出了一个非线性的竞价函数,相比于KDD2012的《Bid Optimizing and Inventory Scoring in Targeted Online Advertising》中提出的线性竞价函数,本文认为出价应该与点击率、转化率等指标具有非线性关系
首先,文章将现实问题用数学方法建模为限制条件下的优化问题,并通过拉格朗日乘子法,求得出价策略的数学表达式(非线性竞价函数);然后利用iPinYou数据拟合出价策略中的参数;最后,做实验验证结果,发现了一个有意思的结论:相比少量高品质的展示机会,那些大量低品质的展示机会同样可以具有较好的广告效果,值得出价。这个发现对于那些预算不够,同时又想做广告的小广告主来说,简直就是福音。
模型建立
选择合适的出价策略,在预算的限制下实现广告效果最大化
把这句话用数学的形式表达出来就是下面的样子:
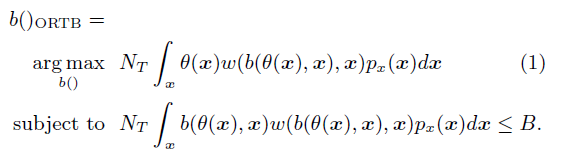
看起来来有点复杂,其实很简单,两个式子,第一行是优化目标:寻找似的收益最大化的出价函数b()
第二行就是预算约束,就是花的钱不能超过预算约束B
模型中涉及的具体符号定义如下:

结合着具体的符号定义,可以解释一下之前建立的数学模型了
$dx$:x代表一次bid request,也就是一次竞价请求的特征向量,是ADX发给DSP的竞价请求“标识XXX,男性,20-25岁,跑鞋爱好者,广告位为首页”,即一次广告展示机会。之所以是dx而不是x,是因为我们关注的是整个广告推广计划中所有的竞价过程,而非某一次竞价。
$p_x(x)$:广告展示机会的概率密度分布,我的理解是在全网所有的竞价中,满足我DSP要求的、或者是我能收到的bid request所占的比例。因此,$p_x(x)*dx$的物理意义是我能收到的展示机会。
$\theta(x)$:θ是赢得此次竞价所能带来的收益(KPI),本文用CTR来衡量,CTR越高,收益就越高。
$b(\theta(x),x)$:对于此次展示机会,在能带来收益为θ(x)的情况下,我所出的价格bid。
$\omega(b(\theta(x),x),x)$:对于此次展示机会,在能带来收益为θ(x)的情况下,我的出价bid能获胜的概率是多少。因此,$\omega(b(\theta(x),x),x)p_x(x)dx$表示对于本次我所收到的这个展示机会来说,在该机会能带来收益(如CTR,CVR等)为θ(x),我出价为bid的情况下,我能打败对手获得此次展示机会的概率。
以$\theta(x)\omega(b(\theta(x),x),x)p_x(x)dx$的物理含义是我出价为bid,赢得这次展示机会后,所能获得的收益。
以$b(\theta(x),x)\omega(b(\theta(x),x),x)p_x(x)dx$的物理含义是我出价为bid,赢得这次展示机会所花费的钱。
$N_T$:生存时间T内广告推广活动中所有的bid request数量
总之还是那句话:选择合适的出价策略,在预算的限制下实现广告效果最大化
模型求解
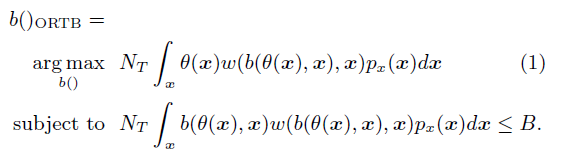
经过一系列的化简,我们可以把模型的函数表达式简化成下面的样子,具体过程参考原文
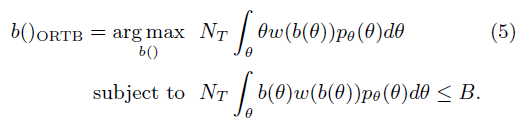
现在参数就只有$\theta$了,也就是CTR,接下来要怎么求解最大值呢?这是要一个带约束条件的最优化问题,作者是用了拉格朗日乘子法来解决的
通过拉格朗日乘子法,我们可以将不等式乘一个参数$\lambda$后和等式写进一个公式里(化简过程已省略),得到如下结果:
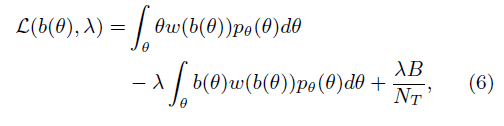
然后对其求导,令导数为0得到:
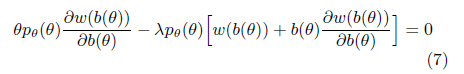
进而求得出价函数$b(\theta)$与赢得竞价概率之间的函数关系为:
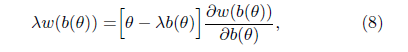
也就是说,我们想要的出价函数b()与胜率函数w()有关,那我们就来看看他们之间到底有什么关系。作者利用数据集绘制出二者之间的关系如图:
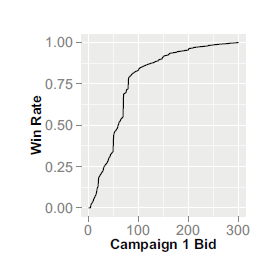
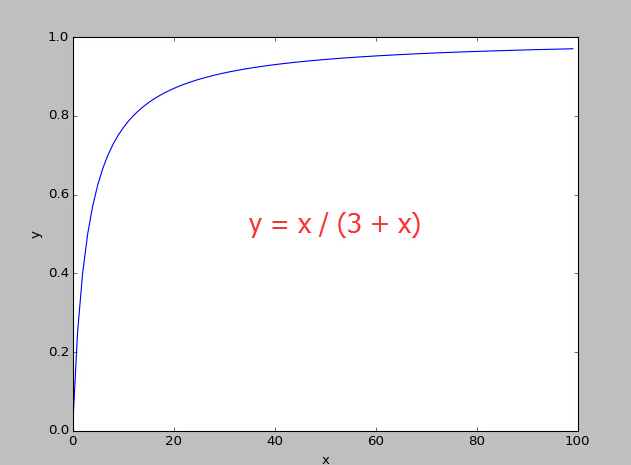
我们发现这个函数走势很像$y=\frac{x}{c+x}$啊!!!对,作者也发现了,于是乎就有了下面的非线性竞价函数:
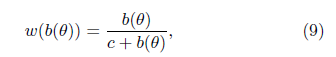
然后把(9)带回到(8)中就求得了我们梦寐以求的非线性出价函数:
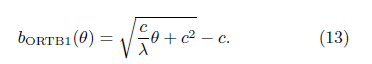
画个图看看上面的两个函数走势吧:
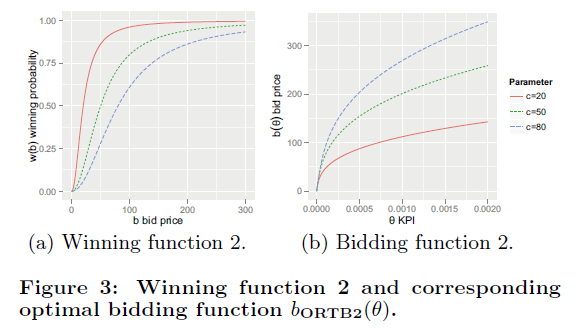
还是很符合实际情况的,点击率越高,出价也就越高,出价越高,赢得竞价的可能行也就越高
到此,我们就已经把问题的数学转化和模型求解弄完了,那剩下的关键问题就是要求解两个参数:$\lambda$和$c$了
可以看出来$c$是可以直接根据历史数据拟合出来的,利用最小二乘法使得均方误差最小即可
难点在于$\lambda$的求解,文章采用的方法是:通过不断调整以获得在测试数据中得到最大收益(点击量)来获得
实验分析
- 利用iPinYou实时竞价数据,每一条数据是一个竞价请求,包含其特征、赢得竞价的价格、用户反馈(点击or转化)
- 将数据集按2:1分割分别作为训练和测试集
- 流程:用训练数据训练出点击率预估模型和出价函数,根据测试数据特征,计算出一个出价,如果超过数据集中的真实出价,则认为竞价成功
- 根据真是数据集中的情况进行模型评估
- 为了对比,将预算分别设置为原始预算的1/64,1/32,1/16,1/8,1/4,1/2进行实验
- 对比策略:按固定值出价,随机出价,按最大eCPC出价,线性出价
经过一系列的实验,文章得出了下面的结论:
- 非线性出价策略赢得的总点击量大,而且单次点击所产生的费用低
- 预算约束越严格的情况下,相比于线性出价策略,非线性出价策略对于点击量的提升越大
- 预算越低,$\lambda$的最优解的值越大,出价相对也越低,但是对于低价值的展示机会,非线性出价策略的出价比线性出价策略的出价略高。如下图所示
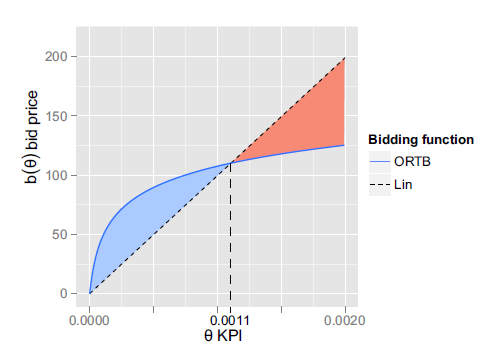
我们可以很直观的看出,我们所得到的出价策略是一个非线性的。横坐标θ代表了广告展示计划的品质,ORTB会对低价值的展示机会出高价,这样的结果能为我们带来什么,谁会去要那些低价值的展示机会呢?我们来看下面这张图
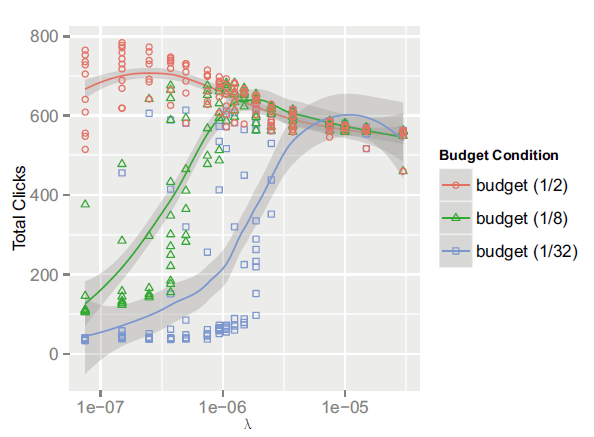
在此图中,我们盯着一条曲线看,比如蓝色的(1/32)。随着λ增加,收获的点击量是增加的,意味着λ越高,我们的收益越高。对于我们获得的出价策略而言,λ越高,我们的出价是越低的,也就意味着这次展示机会的价值是很低的。这样的结果值得我们深思,我们以为低价值的展示机会是不值钱的,但数据说明,这些看似不值钱的展示所能带来的回报还算不错。特别地,在λ=1e-05时三条曲线的几乎重合,而红色代表有钱的广告主,蓝色代表穷广告主,虽然预算差了16倍,但是获得的收益是相同的,这个结论对于预算有限的小广告主而言,是个天大的好消息:虽然我们钱不多,但只要我们出价合适,依然可以收获很好的广告效果,四两拨千斤,极大的调动了小广告主参加程序化交易的积极性。