【算法导论】动态规划（一）钢条切割

发表于 | 分类于 | 浏览 次
字数统计: 1,389 | 阅读时长 ≈ 6

1. 动态规划（Dynamic programming）

这里programming指的是表格，而非编程。动态规划通常用来求解最优化问题

与分治法对比：

  1. 相同点：都是通过子问题组合求解原问题
  2. 不同点：分治法将问题划分为不相交的子问题，求解再合并，动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题，此时如果用分治法就会出现重复计算求解。为了避免重复动态规划对子问题只求解一次，将其保存在表格中，从而无需每求解一个子子问题时重复计算。

2. 求解步骤

  1. 刻画最优解的结构特征
  2. 递归定义最优解的值
  3. 计算最优解的值，通常采用自底向上的方法
  4. 利用计算出的信息构造最优解

其中不是所有的题目都会要求4，仅仅要求3，要求4的时候，我们需要在得到3的同事维护一些额外的信息来求出4。

看到这四个步骤的时候，还是挺懵逼的，继续往下看=.=

3. 钢条切割问题

问题

Serling公司购买一根长钢管，将其切割成短钢管出售，给定钢管长度和对应的价钱如下表：

问题要求根据上面的价格，给出最佳的切割方案，使得收益最大。

以n=4为例，可以将钢条切割成如下图所示的8种情况，其中收益岁大的是(c)：

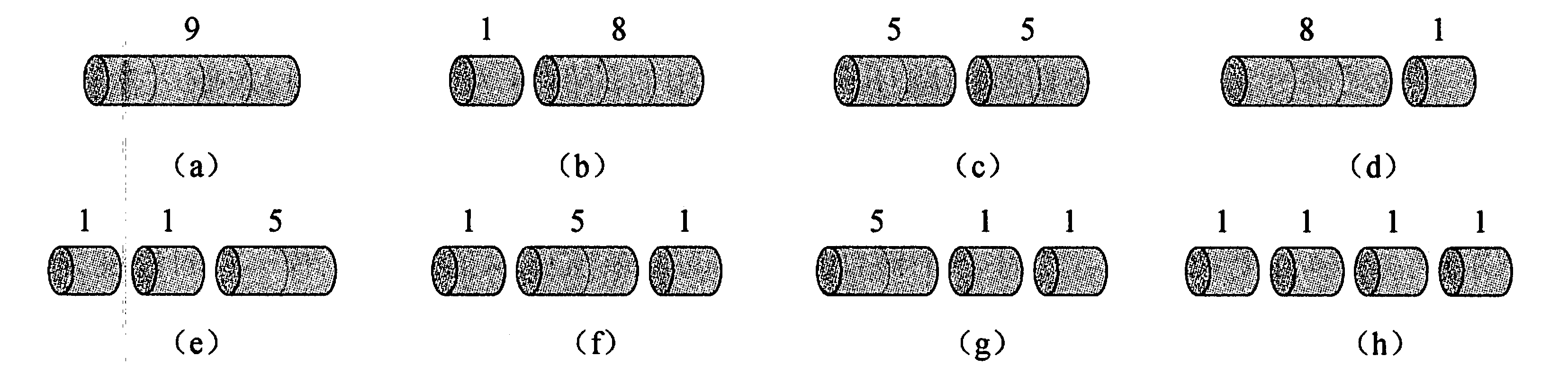
思路

钢条长度为n时，共有$2^{n-1}$种分割方式。

  1. 递归

    把长度为n的钢条切割问题转化为：将钢条从左边切下长度为i的一段，对右边剩下的长度为n-i的钢条进行进一步的切割。

    CUT-ROD(p,n)//p:价格数组，n：钢条长度
    1 if n==0:
    2 	return 0
    3 q=MIN
    4 for i = 1 to n:
    5 	q=max(q,p[i],CUT-ROD(p,n-i))
    6 return q

    当n=4时，上面递推方式的工作量如图所示，复杂度为$T(n)=2^n$

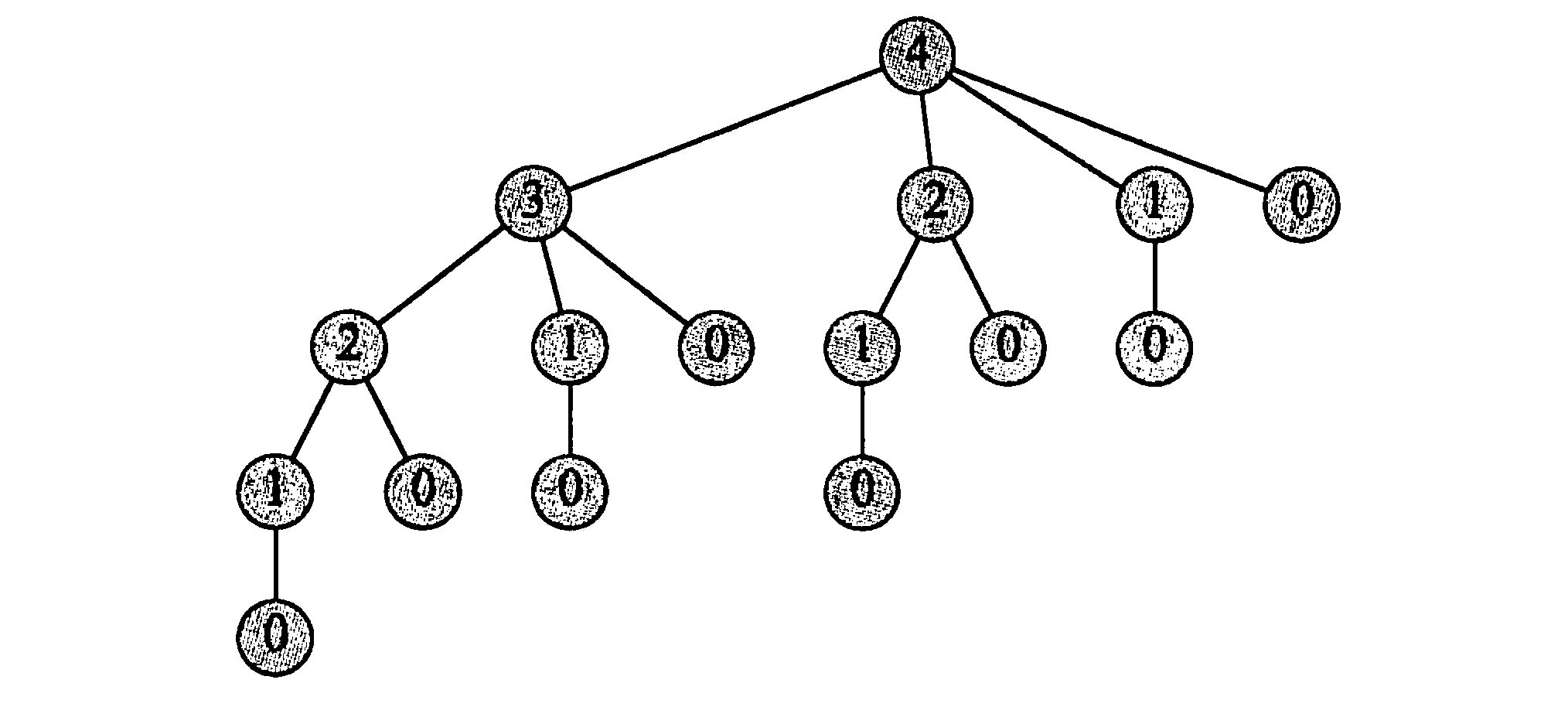
  2. 动态规划（DP）

    可以看出来用上面递归的方式计算，中间会重复求解相同子问题。使用动态规划，仔细安排求解顺序，对每个子问题只求解一次所以，并把结果保存下来，供后续使用避免重复计算。

    ​ 对于钢条切割的问题，我们可以将长度为n的钢条切割问题转化为规模更小的子问题：当完成首次切割后，将两段钢条看成两个独立的钢条切割问题，通过组合两个相关子问题的最优解，选取组合收益最大者，构成原问题的最优解。

    因此，将长度为n的钢条切割成两段，共有下面n种切割方式，求解下面n个子问题的最优解，再选取其中最大的作为原问题的最优解。

    ​以n=4为例：

    $r_1=1$

    $r_2=max(p_2,max(r_1)+max(r_1))=max(5,1+1)=5$

    $r_3=max(p_3,max(r_1)+max(r_2))=max(8,5+1)=8$

    $r_4=max(p_4,max(r_1)+max(r_3),max(r_2)+max(r_2))=max(9,8+1,5+5)=10$

    …

    ​ 动态规划两种实现方法：

  • 自顶向下：

    仍按照递归的方式实现，过程中保存每个子问题的解，后续过程中先检查是否已经保存过此解，如果是，直接返回保存的值。就好像带了一个“备忘录”。

    memorized-CUT-ROD[] = MIN//用于记录子问题结果
    CUT-ROD(p,n)//p:价格数组，n：钢条长度
    1 if memorized-CUT-ROD[n] > 0:
    2 	return memorized-CUT-ROD[n]
    3 else
    4 	for i = 1 to n:
    5 	q=max(q,p[i],memorized-CUT-ROD(p,n-i))
    6 memorized-CUT-ROD[n] = q

    ​

  • 自底向上

    需要恰当定义子问题的“规模”，使得任何子问题的求解都只依赖于“更小的”子问题，进而将子问题按规律排序，按由小到大的顺序进行求解，当求解某个自问题时，它所以来的子问题都已经求解完毕。

    伪代码略，直接上代码：

    int cut_rod(vector<int> p,int n){
        int len = p.size();
        vector<int> maxvalue(len,0);
        for(int i = 0;i < n;i++){//i=n-1
            maxvalue[i] = p[i];
            for(int j = 1; j <= (i+1)/2;j++){
                maxvalue[i] = max(maxvalue[i],maxvalue[j-1]+maxvalue[i-j]);
            }
        }
        return maxvalue[n-1];
    }

    至此，可以求出该问题的最优解了~

重构解

​ 上面的求解过程可以求出最优解的值，但并没有返回解本身（具体的切割方案），为了得到最优解，需要在求解最优解的同时，保存切割信息。扩展上面的算法，使之对子问题不仅保存最优收益值$r_j$，还保存该最优方案对应的第一段钢条的切割长度，也就是第一段钢条的切割位置距离钢条左端的长度$s_j$，最后输出最优方案时，根据$s_j$即可复原出最优解。

int cut_rod(vector<int> p,int n){
    int len = p.size();
    vector<int> maxvalue(len,0);//记录最优方案值
    vector<int> leftlen(len,0);//记录第一段钢条距左端距离
    for(int i = 0;i < n;i++){//i=n-1
        maxvalue[i] = p[i];
        leftlen[i] = i+1;
        for(int j = 1; j <= (i+1)/2;j++){
            if(maxvalue[j-1]+maxvalue[i-j]>maxvalue[i]){
                maxvalue[i] = maxvalue[j-1]+maxvalue[i-j];
                leftlen[i] = j;
            }
        }
    }
    //输出最优解方案
    int m = n-1;
    while(m>=0){
        cout<<leftlen[m]<<"\t";
        m -= leftlen[m];
    }
    return maxvalue[n-1];
}

结果如图：

​