堆
基本性质
支持操作:Add /Remove/Min or Max
heap可以用来求最大值或者最小值,不能同时求最大和最小值。
Heap结构:
一颗尽量填满的二叉树,每次插入节点时,插到最后一行的最左端的空余位置,如果本层没有空余位置了,另起一行。因此节点数目为N的堆对应的二叉树高度为
MaxHeap vs MinHeap
- MaxHeap:父亲节点比左右孩子都大
- MinHeap:父亲节点比左右孩子都小
因此当取最大或最小时,将root值取出即可,因此getMin/Max的时间复杂度为
堆的存储
由于我们需要频繁的对堆进行增加删除,所以一般堆的底层都是通过数组来实现(而不能用链表,因为链表需要频繁new 或 delete对象,非常慢)
对于元素A[i]:
- 父节点:A[i-2/2] (右移1)
- 左孩子:A[2i+1] (左移1,可得到2i)
- 右孩子:A[2i+2] (左移1,低位+1,可得到2i+1)
插入操作
例子:在最小堆中插入元素:1↙ ↘2 3插入0,因为第二行已经满了,加入到第三行最左边:1↙ ↘2 3↙0此时这个堆已经不满足最小堆的条件(父亲节点都比孩子小)了,因此,先交换0和2:1↙ ↘0 3↙2此时仍然不满足最小堆条件,继续交换:0↙ ↘1 3↙2此时满足最小堆条件了,因此,需要交换最多 O(logN)次,插入的时间复杂度为O(logN)
删除操作
例子:在最小堆中删除元素:1↙ ↘3 2↙ ↘ ↙ ↘4 5 10 100删除堆顶元素1,用堆中最后一个节点替换堆顶元素:100↙ ↘3 2↙ ↘ ↙4 5 10此时这个堆已经不满足最小堆的条件(父亲节点都比孩子小)了,因此将堆顶元素下沉,选择左右孩子中较小的交换:2↙ ↘3 100↙ ↘ ↙4 5 10此时仍然不满足最小堆条件,继续交换:2↙ ↘3 10↙ ↘ ↙4 5 100好了,删好了PriorityQueue支持 删除堆顶元素,但对于删除除root外的任意一点的操作,PriorityQueue的时间复杂度会降到
Java中还有另外一种数据结构TreeMap,支持 删除任意元素,而且支持同时获取最大和最小。
TreeMap是一平衡二叉搜索树,因此插入和删除任意元素的时间复杂度都是
| | 用 | 原理 | 实现 |
| ——————- | —— | —————- | —— |
| TreeMap | 必会 | 平衡二叉搜索树,红黑树 | 不需要 |
| PriorityQueue | 必会 | heap,二叉树 | 选做 |
实现
构建堆,堆维护
上面提到了增加和删除节点的操作,下面通过实例说明如何从一个数组开始构建一个堆:
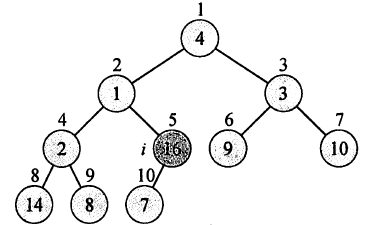
假设我们有数组4,1,3,2,16,9,10,14,8,7
它的形状为:
当然最暴力的方式就是从最后一个元素【7】开始,向上以此对树进行维护。但事实上由于后[n/2]个元素都是根节点,不需要进行维护。因此我们只需要维护前[n/2]个节点。
具体步骤如下图所示:
伪代码为:
|
根据上面的方法,我们可以将一个数组构建成一个堆,堆顶的元素是最大的。
代码:
|
时间复杂度分析:
在高度为h的结点上运行MAX-HEAPIFY的代价是O(h)O(h),因此建树的总代价为:
因此堆排序的时间复杂度为
删除节点POP
|
插入节点
|
堆排序
堆排序就是利用堆的性质,依次将堆顶元素出堆,每次堆顶元素出堆之后堆会自动维护,所以可以保证弹出的节点是有序的。
|
时间复杂度:
n次出堆,每次出堆维护时间logn
HashHeap
哈希堆,Hashheap是用一个hashMap优化了的heap,方便快速定位某个值在heap中的位置。与heap相比,HashHeap多了一个用来指示元素位置的索引。
HashHeap的结构有点特殊,很神奇,需要多看几遍,其中包括两个结构heap和hashmap:
- heap存储元素的值
- HashMap存储元素在heap中对应的位置和出现的次数
这里存储出现次数是因为,有些时候,堆中可能会有重复的元素,如果只存储其位置的话,某个值就会在多个位置上,需要用一个链表来存储所有的位置,这样不仅存储起来不方便,计算也很不方便,所以很巧妙地,我们将同一个值的元素都放到heap中的同一个位置,在hashmap中存储该位置有多少个该元素,这样堆中的每个节点元素的值也不相同了,各种计算操作起来也方便了,完美~
java实现
|
leetcode 相关习题
Trapping Rain Water
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
For example,
Given[0,1,0,2,1,0,1,3,2,1,2,1], return6.
向柱子中灌水,求能够灌水的总量。
分析
可以从边缘向内灌水,灌水的高度不会超过边缘柱子的高度的最小值,所以说:边缘高度奠定了灌水的基调
从低的一边(高度为h)向内灌水,能够灌水的量为(h-h_temp),遇到更高的柱子时,更新边缘。
显然,这是一个双指针问题。

开始时,令总水量sum=0,双指针指向边缘,左选择较小的向内移动,假如选择左边指针。

sum += 1,指针继续向右移动

此时左边指针遇到了跟高的边缘,右边指针开始向内移动

右边指针也同样遇到了更高的柱子,此时再从左右两边指针中选择一个较小的向内移动,假如选的依然是左边的,向内移动,更新sum,知道遇到更高的柱子

右侧指针左移,直到两指针相遇。
代码
|
Trapping Rain Water II
Given an
m x nmatrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.Example:
>
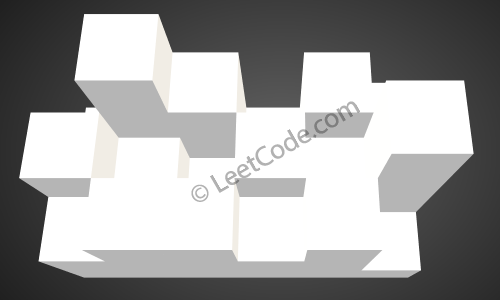
The above image represents the elevation map[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]before the rain.
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.
分析
这一题是上一题在二维空间上的扩展。
对比上一题的思路,上一题的围墙是左右两边的柱子,而这道题的围墙是矩阵四周一圈的墙。我们可以从最矮的墙头向内灌水,然后将被灌水的位置加入围墙。
有两个要解决的点:
- 找到围墙中最矮的墙头
- 从最矮的墙头向围墙内灌水,要知道那边是围墙“内”
对于第1点,要求围墙中最矮的墙头,且墙头是动态插入的,可以维护一个最小堆,每次出堆元素即为最小的。
对于第2点,可以额外维护一个标记数组,记录是否已经被访问过,每次入堆就将该点对应的位置标记,若某一点没有被标记则是在围墙内。
以上图为例:
首先将四周设为围墙,将围墙元素入堆[1,4,3,1,3,2,3,4,2,3,3,2,3,1]

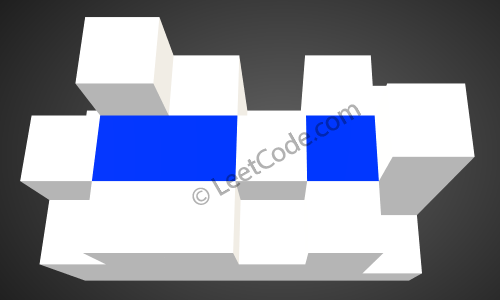
选取围墙中最小的,向内灌水,比如:

由于3>1,不能灌水,将3所在位置加入围墙[1,4,3,1,3,2,3,4,2,3,3,2,3,1, 3]

然后依次选取高度为1的其他几个围墙作为最矮的围墙,发现都不能够往里灌水,接下来选择高度为2的围墙,发现也不能向内灌水了,选取高度为3的围墙,比如:

发现可以灌水量为2,然后将此点灌水后的高度加入围墙,[1,4,3,1,3,2,3,4,2,3,3,2,3,1,3, 3]:

继续重复上边的步骤,知道堆为空
代码
|
Top K Frequent Words
题目
Given a non-empty list of words, return the k most frequent elements.
Your answer should be sorted by frequency from highest to lowest. If two words have the same frequency, then the word with the lower alphabetical order comes first.
Example 1:
>
Example 2:
>
Note:
- You may assume k is always valid, 1 ≤ k ≤ number of unique elements.
- Input words contain only lowercase letters.
Follow up:
- Try to solve it in O(n log k) time and O(n) extra space.
给定一个字符串数组,要求返回出现次数最多的前K个字符串,如果遇到多个字符串年出现次数相同时,则优先取字典序小的字符串。
分析
正常的能够想到的思路是用一个hashmap记录每个单词出现的次数,然后放入一个堆中,堆的排序依据是出现次数多的排在前面,出现次数一样多的,字典序小的排在前面,将全部字符放入堆之后弹出前K个,就得到了出现次数最多的前K个,复杂度:
follow up : 要求我们用时 ,也就是说我们只需要维护大小为K的堆,因此,我们应该采用“最小堆”而非“最大堆”,堆顶元素是当前出现次数最小的,所以当下一次有新元素加进来的时候,如果堆的大小超过了k,就可以把堆顶这个出现次数最少的元素弹掉了,这样一来,最后堆中剩下的k个元素都是出现次数最多得了,是不是很神奇~!!!!
所以这道题我们的堆应该是这样的:
- 出现次数少的优先出堆
- 出现次数一样的,字典序大的优先出队
- 堆的大小为k,当堆中元素个数超过k时,手动poll出堆
这样一来,堆的大小就一直都只有K,时间复杂度就降到 了。这在数据量很大的情况下是十分有必要的!!比如我们要在100亿个数字中找到最大的K个,如果用之前的建堆方法就要建一个100亿大的堆。。。超恐怖,但现在,无论多少数据,我们的堆也只有k那么大了
代码
PriorityQueue:
|
HashHeap:
|
Deque双端队列
可以从两端进行插入和删除
Sliding Window Maximum
题目
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
For example,
Given nums =[1,3,-1,-3,5,3,6,7], and k = 3.
>
Therefore, return the max sliding window as
[3,3,5,5,6,7].
给定数组和窗口大小,要求返回窗口滑动过程中每一个位置的最大值。
分析
方法一:
两层循环,找窗口k内的最大值,时间复杂度
方法二:
维护一个heap,窗口向前滑动时,加一个元素,减一个元素,堆顶元素即为窗口内最大元素,时间复杂度:
方法三:双端队列Deque
我们用双向队列可以在O(N)时间内解决这题。当我们遇到新的数时,将新的数和双向队列的末尾比较,如果末尾比新数小,则把末尾扔掉,直到该队列的末尾比新数大或者队列为空的时候才住手。这样,我们可以保证队列里的元素是从头到尾降序的,由于队列里只有窗口内的数,所以他们其实就是窗口内第一大,第二大,第三大…的数。保持队列里只有窗口内数的方法和上个解法一样,也是每来一个新的把窗口最左边的扔掉,然后把新的加进去。然而由于我们在加新数的时候,已经把很多没用的数给扔了,这样队列头部的数并不一定是窗口最左边的数。这里的技巧是,我们队列中存的是那个数在原数组中的下标,这样我们既可以直到这个数的值,也可以知道该数是不是窗口最左边的数。这里为什么时间复杂度是O(N)呢?因为每个数只可能被操作最多两次,一次是加入队列的时候,一次是因为有别的更大数在后面,所以被扔掉,或者因为出了窗口而被扔掉。
代码
|